Use place value

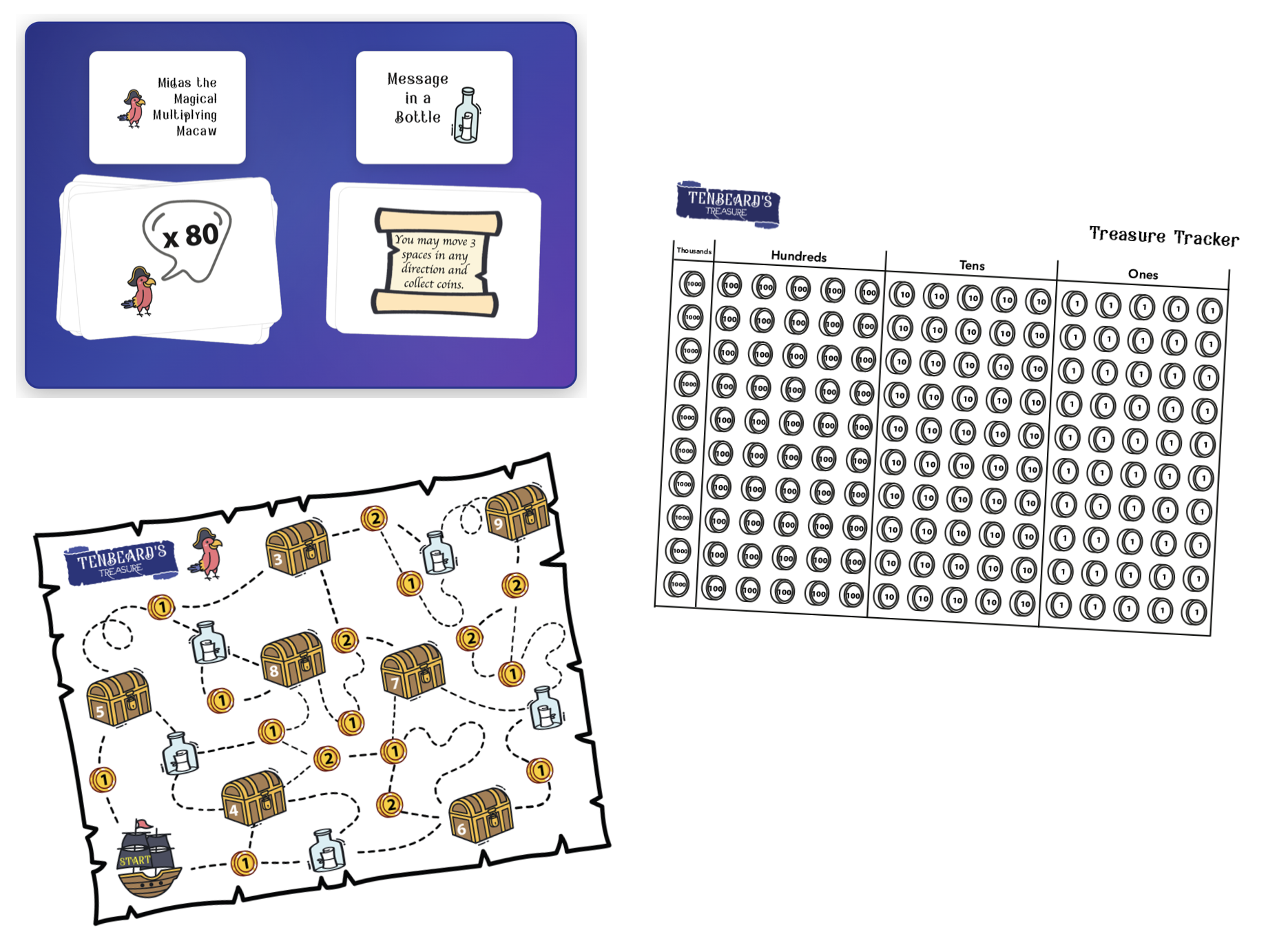
Most upper elementary students can multiply reasonably well and understand place value in isolation, but connecting these ideas takes deliberate practice. Tenbeard's Treasure creates that practice by having students multiply constantly—then immediately deal with the place value consequences of their products.

Here's how it works. Students move around a board collecting coins (values like 1, 2, 4, 7, 9). When they land on a coin or treasure chest, they draw a Macaw card showing a multiplier. Land on a 7-coin space and draw ×40? That's 280 coins to add to your treasure tracker.

The treasure tracker is where the place value work happens. It's a large grid with four columns—thousands, hundreds, tens, ones—each containing 10 rows of 10 circles. Students shade circles to track their treasure. Recording 280 coins means shading 2 hundreds, 8 tens, and 0 ones.

Each column holds exactly 10 rows—forcing students to regroup when they accumulate ten in any position.

This constraint forces regrouping. If you have 12 ones, you must swap 10 of them for 1 ten. The physical act of crossing out 10 circles in the ones column and shading 1 circle in the tens column makes the exchange concrete. Ten ones literally become one ten. Students who've been mechanically "carrying the one" in addition algorithms suddenly see why that works—the digit moves because 10 units in one place equals 1 unit in the next place.

Multiplying by multiples of 10 (like ×30 or ×70) requires decomposing the multiplier. To find 8 × 30, students typically calculate 8 × 3 = 24, then multiply by 10 to get 240. The tracker confirms this: 24 tens is the same as 2 hundreds and 4 tens. The representation flexibility—seeing 240 as "24 tens" or "2 hundreds and 4 tens"—is mathematically important and often glossed over in traditional instruction.

Competition adds useful pressure. Students want to calculate quickly and accurately because errors cost treasure. This motivates efficiency. Early in the game, students might shade 30 individual ones; later, they recognize they can shade 3 tens immediately. This shift from counting to place value reasoning is the pedagogical goal.

The game ends unpredictably—when someone draws the Tenbeard card from the deck. This variability means students work with different magnitudes. Some games yield totals in the hundreds; others reach several thousand. The final score calculation requires reading the entire place value notation: 3 thousands + 2 hundreds + 4 tens + 6 ones = 3,246 coins.

Message in a Bottle cards occasionally disrupt the multiplication pattern by offering bonuses ("collect 30 extra coins") or extra moves. These cards require students to shift between multiplication and addition, maintaining accuracy across different operations.

Fluency with multiplication facts matters, but understanding why algorithms work matters more. Tenbeard's Treasure addresses both. Students get extensive multiplication practice—typically 10-15 problems per game—but the practice is contextualized. Each product represents treasure collected, so students care about accuracy.

The regrouping work builds proportional reasoning that students will need later. When they exchange 10 ones for 1 ten, they're working with a 10:1 ratio. This same structure appears in decimals (10 tenths = 1 whole), fractions (10/10 = 1), and metric conversions (10 millimeters = 1 centimeter). The physical act of swapping makes the ratio concrete rather than abstract.

Strategic thinking develops naturally. Students notice that landing on treasure chests (higher coin values) with large multiplier cards yields more treasure. This requires mental estimation: recognizing that 9 × 50 beats 2 × 20 without computing exact values. Estimation is often taught as a separate skill, but here it emerges from gameplay incentives.

Shading 4 complete rows of tens means seeing 40 as both a geometric pattern and a numerical quantity.

Students who shade 4 complete rows of tens are seeing 40 as both a geometric pattern and a numerical quantity. This connection between visual arrangement and number value supports algebraic thinking later—recognizing that different representations can express the same relationship.

The game also reveals which students genuinely understand place value versus those who've just memorized procedures. Watch for students who need to count individual circles to determine totals, or who don't recognize that 5 hundreds equals 500. These students need more foundational work with place value before moving to algorithms.

Notation flexibility becomes visible. The quantity 250 can appear as 2 hundreds + 5 tens, or as 25 tens, or theoretically as 250 ones (though the tracker would force swapping). Understanding that these representations are equivalent is harder than it looks—students often think there's only one "correct" way to express a number.

Computational fluency develops through repetition, but the game avoids the tedium of worksheets. Students willingly play multiple rounds, accumulating far more multiplication practice than they'd tolerate in drill format. The emotional engagement of competition transforms practice into something students seek out rather than endure.

Use the game after introducing multiplication and place value concepts, not for initial instruction. It provides applied practice and reveals whether students can coordinate multiple skills simultaneously. Students who struggle during gameplay need more foundational work with either multiplication facts or place value structure before attempting combined tasks.

Students need some familiarity with multiplying by ten before this game will be productive.

Materials are straightforward: each player needs a token, a printed treasure tracker, and something to shade circles with. The game board sits centrally, and a device displays the digital card generator. Groups of 3-4 work best for classroom use—pairs move too quickly, and larger groups create too much downtime between turns.

Early gameplay is diagnostic. Watch for students who shade 40 as 40 individual ones rather than 4 tens—they're not yet thinking in place value terms. Notice students who struggle to determine where products belong on the tracker—they may need more work with number magnitude. These observations are more valuable than the final scores, which depend heavily on luck.

When students dispute whether 8 × 50 equals 400 or 450, let them work it out—peer verification builds reasoning.

When one student claims 8 × 50 = 400 and another argues for 450, don't rush to correct. Let them work it out, perhaps by calculating 8 × 5 = 40 and recognizing they need to multiply by 10 again. Peer verification builds mathematical reasoning better than teacher correction.

Game length varies based on when the Tenbeard card appears. Tenbeard usually appears some time between the 15th and 25th turn of the game.

Extension challenges for faster finishers:

• Calculate totals mentally without counting circles
• Determine what multiplier they'd need to reach the next thousand
• Track which coin/card combinations generate the most treasure

These deepen mathematical thinking without requiring additional materials.

Post-game discussion should focus on strategies, not just who won. Ask: Which multiplication shortcuts did you use? When did you have to regroup? Did you notice any patterns in how products appeared on your tracker? These questions help students articulate the mathematics they experienced during play.

The game is replayable, which is pedagogically useful. Students will play multiple rounds willingly, accumulating far more practice than worksheet-based multiplication drills would provide. After several games, look for students developing efficiency—immediately recording products in appropriate columns, swapping proactively, estimating totals rather than counting every circle. The activity drives the mathematics.