Find factor pairs

Factor Fiction builds fluency with factors and divisibility through strategic elimination. Students repeatedly identify all factor pairs of given numbers, then apply divisibility reasoning to narrow down suspects. The mystery context transforms what could be rote factor identification into purposeful mathematical detective work.

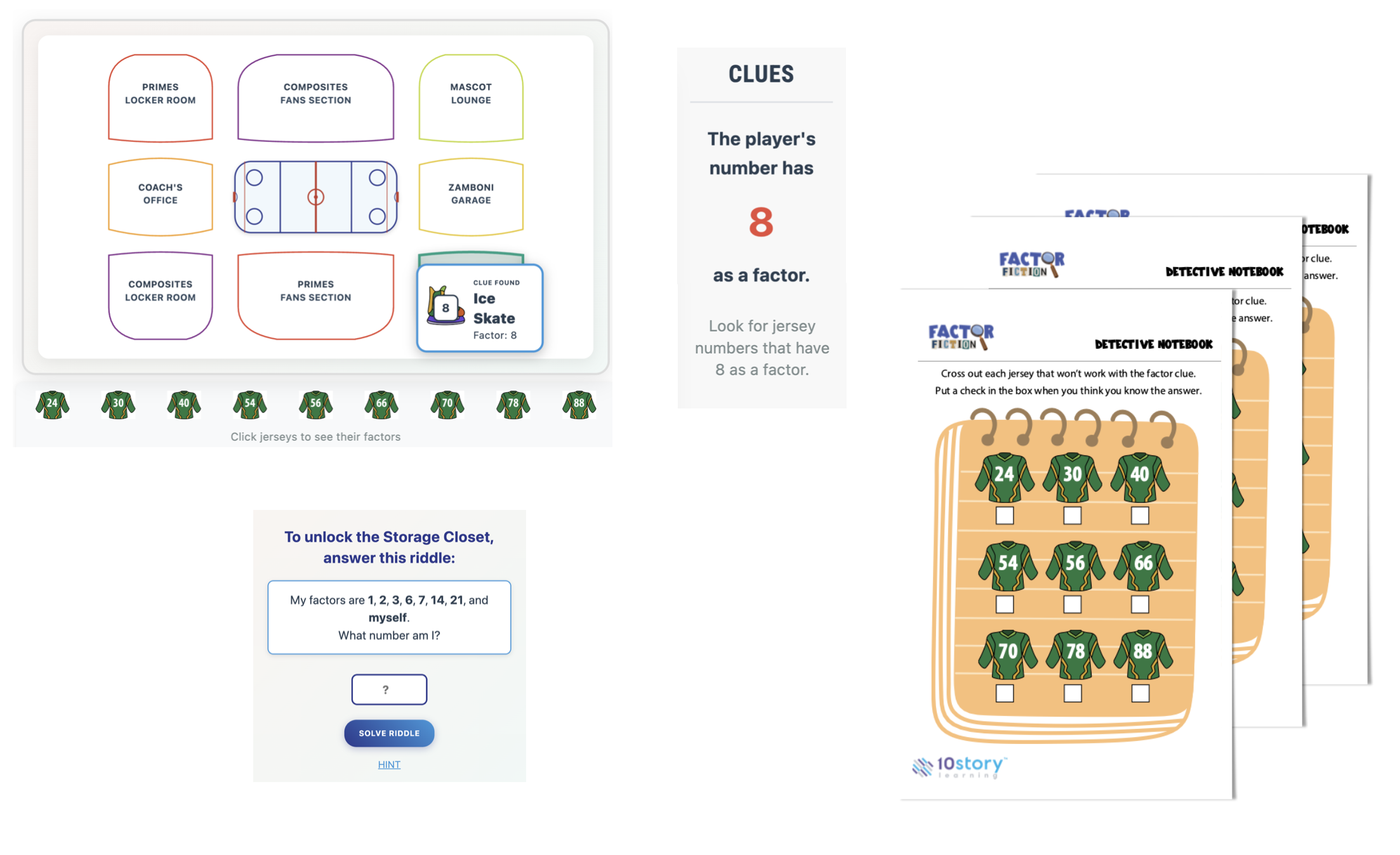
Each room in the hockey arena presents a factor riddle: students must find every factor pair of a mystery number. A factor pair consists of two numbers that multiply together to produce the target number. For 24, the complete set of factor pairs is 1×24, 2×12, 3×8, and 4×6. Finding all pairs requires systematic thinking—students develop strategies for ensuring they haven't missed any factors.

After solving each riddle, students receive a clue identifying a specific factor. They compare this factor against the jersey numbers of all remaining suspects. If the clue states "the thief's number is divisible by 7," students eliminate every player whose jersey number is not a multiple of 7. This process converts factor knowledge into logical deduction.

The elimination mechanic requires understanding divisibility from both directions. When checking if 56 should be eliminated given factor 7, students must recognize that 56 is 7×8—meaning 7 is indeed a factor of 56, so this suspect remains. But 54 cannot be divided evenly by 7, so that suspect is eliminated. This bidirectional thinking—from factors to multiples and back—strengthens number sense.

Finding factors systematically develops as students play repeatedly. Early attempts often involve random guessing—trying multiplication facts until something works. More experienced players develop organized approaches: testing small factors first (2, 3, 5), recognizing that factors come in pairs (finding 4 means 15 must also be a factor of 60), and stopping once they reach a factor pair that repeats (6×6 for 36).

The game exposes students to numbers that challenge common divisibility rules. While rules for 2, 5, and 10 are straightforward (even numbers, ends in 5 or 0), factors like 3, 6, 7, 8, and 9 require either memorization or calculation. Students who have internalized multiplication facts to 12×12 can identify factors quickly. Those still developing fluency practice multiplication relationships in a meaningful context.

Strategic thinking emerges from the elimination process. Clues revealing prime number factors (like 7 or 11) eliminate more suspects than clues about common factors (like 2). Students begin recognizing which clues provide maximum information—if only two suspects remain and both are even, a clue about factor 2 provides no new information. This metacognitive awareness connects mathematical properties to strategic decision-making.

The distinction between factors and multiples becomes operationally clear through gameplay. When students find factor pairs of the riddle number, they're identifying factors. When they check whether jersey numbers are divisible by the clue, they're testing if those numbers are multiples of the clue. This repeated practice with both concepts in complementary contexts builds understanding of their reciprocal relationship.

Factor Fiction develops multiplicative reasoning—thinking about numbers in terms of their multiplicative structure rather than just additive relationships. Recognizing that 56 can be decomposed into 7×8, or into 4×14, or into 2×28, reflects understanding that numbers can be viewed as products of other numbers.

The game naturally introduces prime versus composite number concepts. Some riddle numbers have many factor pairs (like 60 with 1×60, 2×30, 3×20, 4×15, 5×12, 6×10), while others have just two (like 29 with only 1×29). Students notice this pattern and begin distinguishing between numbers with rich factor structures and those with minimal factorization.

Understanding the relationship between multiplication and division deepens through factor work. When students identify 8 as a factor of 56, they're simultaneously recognizing that 56 ÷ 8 = 7. The factor pair 8×7 encodes the same mathematical relationship as the division fact 56 ÷ 8 = 7 and its inverse 56 ÷ 7 = 8. This connection between operations becomes operationally clear through repeated practice.

The elimination logic mirrors conditional reasoning used throughout mathematics. If a number is divisible by 7, it remains under consideration; if not, it's eliminated. This if-then logical structure appears in proof-based mathematics, programming, and scientific reasoning. Students practice applying rules consistently and tracking which conditions have been satisfied.

Students develop intuition about which numbers have many factors versus few. Multiples of 2, 3, and 5 tend to have more factor pairs than numbers with larger prime factors. Numbers that are perfect squares (like 36 or 64) have an odd number of factor listings when written out individually, because one factor multiplies by itself. These patterns become familiar through repeated exposure.

The game also builds working memory and attention to detail. Students must remember which suspects have been eliminated based on previous clues while processing new clues. They practice holding multiple pieces of information simultaneously and applying new constraints to an evolving problem space—cognitive skills that extend beyond mathematics.

Collaborative play introduces mathematical communication. Students must articulate their factor-finding strategies, explain why particular suspects should be eliminated, and justify their final guess. This verbal explanation of mathematical reasoning develops precision in mathematical language and exposes gaps in understanding when explanations don't convince teammates.

Factor Fiction works well after students have been introduced to factors and multiples but need extensive practice to build fluency. The game provides that practice in a context where accuracy matters—errors in finding factors lead to incorrect eliminations and wrong guesses about the culprit.

Students should understand what factors are before playing—that factors of a number divide evenly into that number, and that factor pairs multiply together to produce the number. If students are still developing this understanding, begin with smaller riddle numbers (those below 50) and provide multiplication charts as reference tools.

Group sizes of 2-4 students work effectively. Pairs encourage both students to participate actively in factor-finding and elimination. Larger groups provide more diverse mathematical thinking but require explicit turn-taking protocols to ensure all students contribute. Within groups, students can divide tasks—one student identifies factor pairs, another checks them, a third marks eliminations on the notebook.

Before students' first game, demonstrate a systematic approach to finding all factors: start with 1, check if 2 divides evenly, continue through potential factors up to the square root of the number. Emphasize that factor pairs mirror each other—once you've checked up to the square root, you've found all factors. This prevents the common error of finding some factor pairs but missing others.

Early games often involve errors—students miss factors, incorrectly eliminate suspects, or forget which clues they've received. Rather than treating these as failures, use them as learning opportunities. When a team makes an incorrect final guess, ask them to review their eliminations: did they miss any factors in the riddles? Did they correctly apply divisibility tests to each suspect?

The digital component generates different mystery scenarios each game, preventing memorization and ensuring continued engagement. The randomization means teachers don't need to prepare multiple variants—the system provides essentially unlimited unique mysteries. However, students benefit from discussing general strategies that apply across games, not just solutions to specific mysteries.

For students who complete games quickly, introduce challenges: solve the mystery using the fewest possible rooms, predict which factor clues would eliminate the most suspects before searching rooms, or identify which jersey numbers share the most factors. These extensions maintain engagement while deepening factor understanding.

Students struggling with factor identification may need supplemental support with multiplication facts or access to factor reference sheets during initial games. As fluency develops, gradually remove these supports. The goal is not to make the game artificially easy but to scaffold students toward independent factor-finding.

The detective theme provides opportunities for creative extension. Students can write their own mystery scenarios, create additional suspect profiles with different jersey numbers, or design factor riddles that provide specific strategic advantages. These creative tasks require understanding factor relationships deeply enough to manipulate them intentionally.

After teams complete their investigations, facilitate reflection: Which clues were most helpful? Why? Did certain suspects get eliminated early? What factors do many of the jersey numbers share? Which numbers have unusual factor structures? These questions connect the specific game experience to broader number theory concepts.

Factor Fiction fits into operations and algebraic thinking units as applied practice in factors and multiples. Students work with authentic problem-solving that requires accurate factor identification, develop fluency through repeated application, and experience how mathematical concepts function as logical tools rather than isolated procedures. Students check their work, ask for help when needed, and persist through challenges. The activity drives the mathematics.